在克拉玛依三坐标测量评价中，经常用到最小二乘、最小区域、更大内切、最小外接等计算方法，那他们分别是如何定义的呢?

　　以2D圆为例：

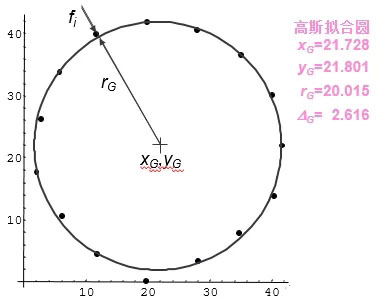
　　(1)最小二乘圆(即高斯圆)：最小二乘法使用最为广泛，最小二乘法是一种数学优化算法，通过最小化误差的平方和找到一组数据的更佳匹配函数，对于最小二乘圆而言，就是找到一个圆使测量的所有点到该圆的距离平方和最小。

　　(2)最小区域圆(即切比雪夫圆)：由两个同心的圆把所有的测量点包含在两圆形成的环形区域内，并且要保证两圆的半径差最小，切比雪夫拟合圆是这两个圆的中值圆，由此可见，存在两个与切比雪夫圆同心且相对距离(半径差)最小的两个圆。所有的提取点都在这两个圆区域范围内(最小区域)或者圆上。

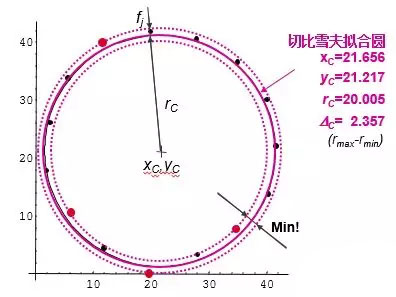
　　最小区域法主要用于形状误差的评价：

　　(2.1)直线度：直线度误差是包含所有提取直线的一对间距最小的平行线之间的距离：如下图，直线度为h3;

　　(2.2)平面度：平面度误差是包含所有提取表面要素的距离最小的两个平行平面之间的距离;

　　(2.3)圆度：圆度误差是包含所有提取要素的同心圆且两圆半径差最小;

　　(2.4)圆柱度：圆柱度误差是包含所有提取表面要素的同轴圆柱且两圆柱半径差最小;

　　(3)更大内切圆：即所有点都在圆外或圆上形成的更大的圆，主要用于内部要素(例如孔)的配合尺寸，内部要素做基准的尺寸;

　　(4)最小外接圆：即所有点都在圆内或圆上形成的最小的圆，主要用于外部要素(例如轴)的配合尺寸，外部要素做基准的尺寸。